Games With Minimax
Background
The minimax algorithm is an algorithm that uses recursion to play a turn based game. The name comes from the basic way the algorithm works, maximizing one player’s value while minimizing the other player’s.
Take a simple game like Tic-Tac-Toe. X starts by playing in the middle. This leaves eight spots for O to choose from. What the minimax algorithm does can then be summed up in four steps.
A Tree made of nodes and edges is defined, where each edge coming off a node is a possible move.
The terminal states are the ends of each branch.
The minimax algorithm then backpropagates to the root node, finding the best move.
The best move is executed.
This then gives player O the most optimal move, assuming that player X also plays optimally.
Tic-Tac-Toe
Let’s look at the minimax algorithm in action. I’ve made a simple Tic-Tac-Toe game that uses this algorithm. Here is the actual minimax function. If you want to see the entire code, you can view it on my github.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def minimax(board, depth, is_maximizing):
winner = check_win_state(board)
if winner == "O":
return 1
elif winner == "X":
return -1
if len(generate_possible_moves(board)) == 0:
return 0
if is_maximizing:
best_value = -float("inf")
for move in generate_possible_moves(board):
board[move[0]][move[1]] = "O"
v = minimax(board, depth + 1, False)
board[move[0]][move[1]] = " "
best_value = max(best_value, v)
return best_value
else:
best_value = float("inf")
for move in generate_possible_moves(board):
board[move[0]][move[1]] = "X"
v = minimax(board, depth + 1, True)
board[move[0]][move[1]] = " "
best_value = min(best_value, v)
return best_value
In this function minimax, the arguments board, depth, and is_maximizing are taken. Winner is set to the output of check_win_state(board), which returns the winner, if there is one, as a string. If there is no winner, it returns none. Then the function gives O winning a value of 1, X winning a value of -1, and a tie a value of 0. The function checks for a tie by seeing if there are any more possible moves, and if not, it’s a tie. Now for the minimax part. If is_maximizing is True, then the best value is set to negative infinity, ensuring that all other moves are better. Then the function goes through each move, and then recursively calls itself, adding one to the depth and switching is maximizing to False. Then it reverts the move and updates best_value using the max function. If is_maximizing is False, then best_value is set to positive infinity, and a similar process occurs. The difference, but the min function is used instead of the max function, because here the function is trying to minimize. Ultimately, the function returns the best value.
But how does this algorithm take the best value and find the move that achieves that value. Another function handles this is, by finding the move that has the best value, using the minimax function.
1
2
3
4
5
6
7
8
9
10
11
12
def ai_move(board):
best_move = None
best_value = -float("inf")
for move in generate_possible_moves(board):
board[move[0]][move[1]] = "O"
move_value = minimax(board, 0, False)
board[move[0]][move[1]] = " "
if move_value > best_value:
best_value = move_value
best_move = move
if best_move:
board[best_move[0]][best_move[1]] = "O"
In this function ai_move, the argument board is taken. The value best_move is set to none and best_value is set to be negative infinity. Then the function uses a for loop to iterate over all moves generated by the function generate_possible_moves. Then for each, it places the O, which is the ai player. Then the minimax function is called with the current board state, the depth set to zero, and is_maximizing set to false. The minimax algorithm then does its thing, and evaluates the outcome of the move. Then the board is returned to its initial state. The variable move_value, which was used to store the minimax result, is checked against the current best_value. If it is greater, then the best_value is updated, and the variable best_move is set to that move. This process continues for all possible moves that are generated. Once outside of this for loop, then if there is a best_move, the move is executed.
There was one more function that I wrote that I also think is pretty cool, however slightly off topic. I didn’t want to play Tic-Tac-Toe with just board[0], board[1], and board[2] printed, because that’s boring. So I made a function that prints the board so that it looks like a Tic-Tac-Toe board!
1
2
3
4
5
6
7
def print_board(board):
print(" ")
for i, row in enumerate(board):
print(" | ".join(row))
if i < len(board) - 1:
print("---------")
print(" ")
This function works by joining the elements of each row in the board by a pipe, and then checks if the row is the last one, and if not, then it makes a bar. I feel like this completes the Tic-Tac-Toe feel!
Here is a full game against the computer where the player is the X and the computer is the O.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| |
---------
| |
---------
| |
Enter your move: 2,2
O | |
---------
| X |
---------
| |
Enter your move: 1,2
O | X |
---------
| X |
---------
| O |
Enter your move: 1,3
O | X | X
---------
| X |
---------
O | O |
Enter your move: 2,1
O | X | X
---------
X | X |
---------
O | O | O
AI wins!
Checkers
I wanted more of a challenge, and I wanted to be able to use another feature of the minimax algorithm, so I decided that checkers would be a good option. It also feels more original, because I feel that everyone makes a Tic-Tac-Toe using minimax. The approach was largely the same, but with a few key differences. The issue is that there are many many possible moves, and so many layers of depth, that it becomes very computationally difficult to iterate through every possible move. This is where my good friend pruning comes in. The pruning for this algorithm is called alpha beta pruning. This mode of pruning seeks to prune branches of the tree if they will not happen.
For example, if the minimizing player sees that its option for one move is a value of 8, if the other side returns anything greater than 8, everything on that branch should be disregarded because it will not produce anything less than 8 then. This is because the maximizing player would choose either that value or a value that is higher than that, so the minimizing player would have to go with that 8. This form of pruning allows for lots of branches to be pruned, when ultimately they would not add anything to the search.
First, I want to show the checkers’ function for generating all valid moves in a current state.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
def get_valid_moves_state(pos, state):
piece = next((p for p in state if p['position'] == pos), None)
if not piece:
return {}
col, row = piece['position']
directions = []
if piece.get('king', False):
directions = [(-1, -1), (-1, 1), (1, -1), (1, 1)]
else:
dr = -1 if piece['color'] == RED else 1
directions = [(dr, -1), (dr, 1)]
normal_moves = {}
capture_moves = {}
for dr, dc in directions:
new_col = col + dc
new_row = row + dr
if 0 <= new_col < 8 and 0 <= new_row < 8:
if not any(p['position'] == (new_col, new_row) for p in state):
normal_moves[(new_col, new_row)] = None
else:
other_piece = next((p for p in state if p['position'] == (new_col, new_row)), None)
if other_piece and other_piece['color'] != piece['color']:
landing_col = new_col + dc
landing_row = new_row + dr
if 0 <= landing_col < 8 and 0 <= landing_row < 8:
if not any(p['position'] == (landing_col, landing_row) for p in state):
capture_moves[(landing_col, landing_row)] = (new_col, new_row)
if capture_moves:
return capture_moves
return normal_moves
First, I want to show the checkers’ function for generating all valid moves in a current state. This function takes the parameters position and state. The function starts by looping through the dictionary state, checking if something matches a position. Then the position is stored in col, row. If the piece is a king, then it can move in all four diagonal positions, but otherwise it can only move up or down depending on the else statement. This is done by checking for the color, and changing the variable dr accordingly. Then there is a check for if the valid diagonal moves are open, and if so they are added to the dictionary normal_moves. If there is another piece that is diagonal to the piece, but it is a different color, that information is then stored to the capture_moves dictionary. Then, according to the most annoying rule in checkers, if there are any capture moves, those are returned, else the normal moves are returned.
Now let’s look at the checkers’ minimaxing function.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
def minimax_state(state, depth, alpha, beta, maximizing_player):
red_pieces = [p for p in state if p['color'] == RED]
black_pieces = [p for p in state if p['color'] == BLACK]
if depth == 0 or not red_pieces or not black_pieces:
return evaluate_state(state)
if maximizing_player:
max_eval = float('-inf')
moves = generate_possible_moves_state(state)
if not moves:
return evaluate_state(state)
for move in moves:
piece, dest, cap = move
new_state = simulate_move(state, piece, dest, cap)
eval = minimax_state(new_state, depth - 1, alpha, beta, False)
max_eval = max(max_eval, eval)
alpha = max(alpha, eval)
if beta <= alpha:
break
return max_eval
else:
min_eval = float('inf')
moves = generate_possible_moves_state(state)
if not moves:
return evaluate_state(state)
for move in moves:
piece, dest, cap = move
new_state = simulate_move(state, piece, dest, cap)
eval = minimax_state(new_state, depth - 1, alpha, beta, True)
min_eval = min(min_eval, eval)
beta = min(beta, eval)
if beta <= alpha:
break
return min_eval
This is a large function, so let’s break it down. First, the function takes the parameters state, depth, alpha, beta, and maximizing_player. This is in a lot of ways similar to the Tic-Tac-Toe, but with a few key differences. First, two lists, red and black pieces, are made and saved to two different variables. Then the function checks if either the depth is zero, or if there are no more of either list of pieces. If so, it returns an evaluation of the state. The evaluation function just looks at the difference in number of pieces, giving extra weight to the kings. The function then does its standard minimax algorithm things, setting min_eval and max_eval to infinity and negative infinity respectively. It calls minimax with maximizing_player set to False and then True. There are a few differences however. First, instead of adding one to the depth like in Tic-Tac-Toe, one is subtracted from the depth. This is because the function cannot go too deep, even with alpha beta pruning. This is because of the amount of time that it takes to compute all the possible moves. The most I was able to do was a search depth of 6, even with the pruning. The second major difference is the updating of the alpha and beta variables, that are parameters of the function minimax_state. for example, in the if statement, there is the line:
1
2
3
alpha = max(alpha, eval)
if beta <= alpha:
break
This sets the variable alpha to the eval variable if it is greater, because of the max function. Then there is an if statement that checks for if the variable beta is greater than or equal to alpha. If so, then it breaks out of the loop, because the branch being explored can be pruned. This same can be seen in the else statement, however there beta is being updated with the min function. This alpha beta pruning allows for the algorithm to prune fruitless branches.
I used pygame for the checkers display itself. Pygame is really easy to use, and a great option for making 2D games in python…like checkers! Here is an active game of checkers using the script with pygame.
 A screenshot of the checkers board at the beginning of the game
A screenshot of the checkers board at the beginning of the game
This is the starting position of the board. I added a few things to make the game feel better. For example pieces that are kings have white circles on top, and the selected piece has a green outline around it.
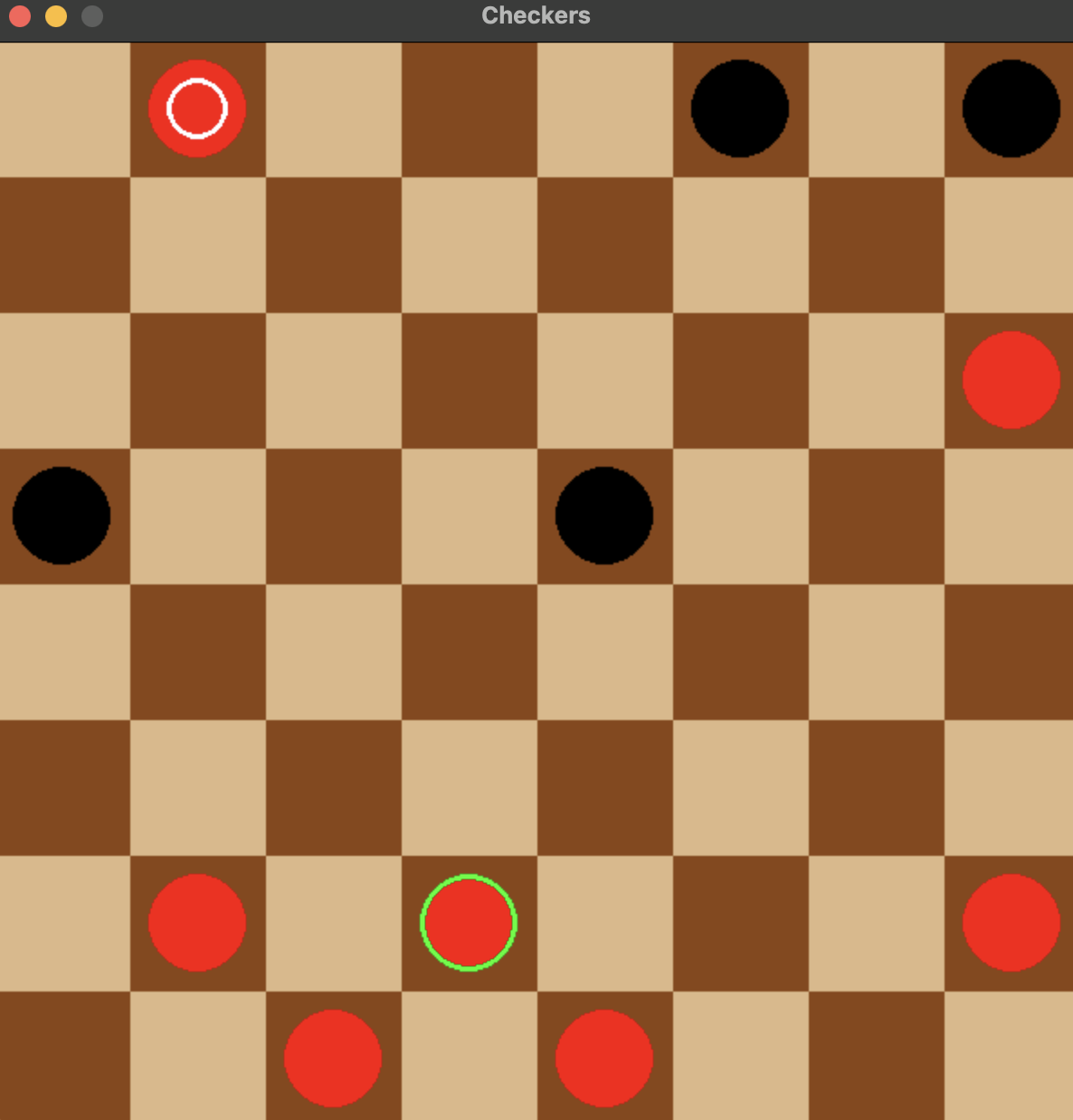 A screenshot of the checkers board in the middle of the game
A screenshot of the checkers board in the middle of the game
Conclusion
And that’s it! I have had a lot of fun making these projects. There is still a lot that I could improve, especially with the checkers game. The Tic-Tac-Toe is currently undefeated (and I doubt that will change), however the checkers game is really easy to beat because the depth of the search is only six. I hope that I will revisit this project in the future, and add a few more things. The minimax algorithm could be optimized more for checkers, and the heuristics could be greatly improved, however I am going to leave the project where it is at for now. The code for both Tic-Tac-Toe and checkers are on my github.
I want to link the YouTube videos that taught me how to use this algorithm. First is John Levine’s video on Alpha Beta pruning. Second is Sebastion Lague’s video on Minimax and Alpha Beta prunning. Third is freeCodeCamp.org’s video for Harvard CS50’s Artificial Intelligence with Python. These videos helped me so much in understanding the algorithm and how it functions.